Отправляйте ваши ответы по адресу: 367000, г. Махачкала, ул. М. Гаджиева, 94, 2-й эт., газета «Черновик» или на e-mail: eruditor@mail.ru.
Список участников проекта за прошлый номер
1. Бастамин Магомедов – 280,5 баллов
2. BOSS – 255 баллов
3. Lord Bizard – 255 баллов
4. alex – 255 баллов
5. Хабиб Халидов – 255 баллов
6. Тагират Магомедова – 255 баллов
7. Ибрагим Газигандов – 255 баллов
8. Абдурахман Сулейманов – 255 баллов
9. Габибуллах Ахмедов – 255 баллов
10. Каримула Шихмурадов – 255 баллов
11. М. Аматгаджиев – 255 баллов
12. Арсланали Эсенбулатов – 255 баллов
13. Валерий Ахмедов – 255 баллов
14. Абдурашид ОБЖ – 255 баллов
15. Уллубий Сулейманов – 255 баллов
16. Kitty – 255 баллов
17. Ибрагим Газимагомедов – 215 баллов
18. dayzy – 215 баллов
19. echo2002@mail.ru – 215 баллов
20. AKC 001 – 215 баллов
21. Салих Салихов – 215 баллов
22. Магомед Гасанов – 215 баллов
23. Камиль Исламов – 215 баллов
24. Ciel77 – 215 баллов
25. Avtor – 215 баллов
26. Абдул Гитинасулов – 215 баллов
27. Шапи Магомедов – 215 баллов
28. Абдулгамид – 215 баллов
29. Камал Залимханов – 215 баллов
30. suslik 01 – 215 баллов
31. Магомедали Мамакаев – 215 баллов
32. Магомед Гитинамагомедов – 215 баллов
33. «Excell» – 215 баллов
34. Махмуд Гаджигереев – 215 баллов
35. Камал Залимханов – 215 баллов
36. Магомед Сулейманов – 160 баллов
37. maga101 – 160 баллов
38. Quik – 160 баллов
39. Магомед Караев – 160 баллов
40. kott kott – 160 баллов
41. Dair Abdulkadirov – 160 баллов
42. Шамиль Ибрагимов – 160 баллов
43. Али Алмасов – 160 баллов
44. Абулмуслим Алиев – 160 баллов
45. Магомед Албасов – 160 баллов
46. Гамид Магомедов – 160 баллов
47. fikret – 160 баллов
48. Джафар Джафаров – 160 баллов
49. М. Амайгаджиев – 160 баллов
50. WILD – 135 баллов
51. zaur85 – 135 баллов
52. Юнусов – 135 баллов
53. Ахмед – 135 баллов
54. Тимур Насиров – 135 баллов
55. arseen babatov – 135 баллов
56. Абдул Алмасов – 135 баллов
57. Сабир Абдулкадыров – 135 баллов
58. mari@mail.ru – 135 баллов
59. Газимагомед Абдуллаев – 135 баллов
60. DANGER_05 – 135 баллов
61. Mustafa Said – 135 баллов
62. Гамзат Алиев – 105 баллов
63. BakS – 105 баллов
64. seena2008@mail.ru – 105 баллов
65. Муслим Закарьяев – 105 баллов
66. Arsen – 105 баллов
67. Ali – 105 баллов
68. aks@mail.ru – 105 баллов
69. Абдула Муслимов – 105 баллов
70. SOMZ – 105 баллов
71. Manas – 105 баллов
Цифры в квадрате 60 баллов
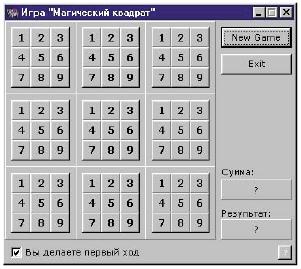
Нужно расположить числа от 1 до 9 в квадрате 3х3 (9 ячеек) так, чтобы суммы чисел в каждом ряду, столбце и диагоналях были одинаковыми.
Физика 100 баллов
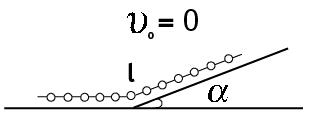
Длинная цепочка, сплетённая из шарнирно связанных мелких звеньев, движется без трения по жёлобу, состоящему из двух частей: горизонтальному и наклонному (рис.). Пройдя половину своей длины по наклонной части жёлоба, цепочка останавливается. До остановки по наклонной части жёлоба цепочка проходит расстояние, равное половине своей длины. Определить время прохождения этого расстояния. Длина цепочки L.
Луч в кубе 80 баллов

Луч света, направленный из вершины куба, отразившись 2008 раз от его внутренних зеркальных стенок (по закону, «угол падения равен углу отражения») и не попадая при этом на ребра, заканчивает свой путь в другой вершине куба. Какое наименьшее расстояние может пройти луч света, если длина ребра куба равна 1?
Ответы на задания предыдущего номера
Что за прибор?
Новый прибор, который работает по такой же технологии, что и зрение омаров (лобстеров), называется The Lobster-Eye X-ray Inspection Device, и производит его американская компания Physical Optics Corporation.
Назвали аппарат в честь некоего абстрактного лобстера LEXID
(Lobster-Eye X-ray Inspection Device) – что в переводе с английского значит «устройство типа глаза лобстера для осмотра с помощью рентгеновских лучей»;
Устройство смотрит сквозь стены благодаря рентгеновским лучам. Марку конфет, которые лежат за стеной магазина, вы, конечно, не увидите, но очертания и их наличие там – запросто.
В чёрном или белом?
Поскольку излучательная способность чёрного тела больше, чем белого, то зимой теплее в белой шубе (в белой шубе тепло, выделяемое человеческим телом лучше сохраняется).
По этой же причине летом прохладнее в чёрной шубе (тепло тела лучше переходит в окружающую среду).
Гора
Теория: высота, на которую забрался альпинист, определяется функциями H=F(t) для подъёма и H=G(t) для спуска.
Условие нахождения на одинаковой высоте соответственно F(t)=G(t).
Следует установить: всегда ли данное уравнение имеет решение в области определения (область определения каждой из функций – время соответствующего процесса – подъёма или спуска).
Однако, поскольку данные функции непрерывны и полностью определены на интересующем нас интервале, при этом одна функция (в целом) возрастающая, а другая – убывающая, причём возрастают и убывают они до одних и тех же величин, точка пересечения существует обязательно, то есть такой момент всегда найдётся!
Решение: а)задачу можно перефразировать: есть два альпиниста, один идёт снизу, другой – сверху. Нужно доказать, что они где-нибудь встретятся.
А встретятся они при этом обязательно. Это и будет искомая точка;
б) подъём и спуск можно представить себе так.
На одной стороне один альпинист забирается на гору, включив таймер. А другой альпинист спускается с горы на другой стороне, также включив таймер, одновременно с первым. В месте одинаковой высоты наших близнецов время тоже одинаковое. Так что ответ: «Всегда».
Клетчатая эпидемия
Теория: Докажем более сильную теорему – n вирусов могут заразить всю доску nXn только в том случае, если все они расположены на большой диагонали доски.
Доказывается методом математической индукции.
При n = 2 теорема справедлива: если два вируса находятся на одной горизонтали (вертикали), то на другую горизонталь (вертикаль) они не смогут добраться.
Пусть теорема верна при n = к.
На доске к + 1 выберем «поддоску» размером к так, чтобы её левый нижний угол совпадал с левым нижним углом доски к + 1. Согласно предположению, индукции «к» вирусов на этой «поддоске» должны находиться по главной диагонали «поддоски».
1. Главная диагональ «поддоски», на которой находятся вирусы, идёт из левого нижнего в правый верхний угол. Если к + 1-й вирус не расположен в правом верхнем углу доски, то либо одна горизонталь, либо одна вертикаль полностью свободны от вирусов и на неё вирусы не проникнут.
2. Главная диагональ «поддоски», на которой находятся вирусы, идёт из правого нижнего угла «поддоски» в левый верхний. Тогда, если к + 1-й вирус не находится в правом верхнем углу доски, случай сводится к предыдущему. Если к + 1 -й вирус находится в правом верхнем углу доски, то вирусы не попадут ни на правую вертикаль, ни на верхнюю горизонталь. На этом можно считать доказательство законченным.
Две двойки
Если считаться с экспонентой expп = п в степени е
1. (2 exp п)2 = 2007
exp п = пе
(2пе )2 = 2017
Здесь всего две цифры «2», но есть экспонента.
2. Поль Адриен Морис Дирак – английский физик, один из создателей теоретических основ квантовой физики, лауреат Нобелевской премии по физике 1933 года – нашёл способ выразить любое натуральное число всего лишь через три двойки и математические операции:
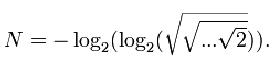
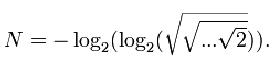
Число знаков корня равно числу N.
В нашем случае:
2 – основание логарифма,
где число знаков корня равно числу 2007.
Номер газеты
- 5 просмотров